සංඛ්යානමය ගැටලු විසඳීම සඳහා එක් ක්රමයක් වන්නේ විශ්වාසනීය පරතරය ගණනය කිරීමයි. කුඩා නියැදි ප්රමාණයක් සහිත ලක්ෂ්ය තක්සේරු කිරීම සඳහා වඩාත් සුදුසු විකල්පය ලෙස එය භාවිතා කරයි. විශ්වාසනීය පරතරය ගණනය කිරීමේ ක්රියාවලිය තරමක් සංකීර්ණ බව සැලකිල්ලට ගත යුතුය. නමුත් එක්සෙල් මෙවලම් මඟින් එය ටිකක් සරල කළ හැකිය. මෙය ප්රායෝගිකව සිදු කරන්නේ කෙසේදැයි සොයා බලමු.
මෙයද කියවන්න: එක්සෙල් හි සංඛ්යානමය කාර්යයන්
ගණනය කිරීමේ ක්රියා පටිපාටිය
මෙම ක්රමය විවිධ සංඛ්යානමය ප්රමාණවල කාල පරතරය තක්සේරු කිරීමේදී භාවිතා වේ. මෙම ගණනය කිරීමේ ප්රධාන කාර්යය වන්නේ ලක්ෂ්ය ඇස්තමේන්තුවේ අවිනිශ්චිතතාවයන් ඉවත් කිරීමයි.
එක්සෙල් හි මෙම ක්රමය භාවිතා කරමින් ගණනය කිරීම් සිදු කිරීම සඳහා ප්රධාන විකල්ප දෙකක් තිබේ: විචලනය දන්නා විට සහ එය නොදන්නා විට. පළමු අවස්ථාවේ දී, ශ්රිතය ගණනය කිරීම් සඳහා යොදා ගනී TRUST.NORMදෙවනුව - විශ්වාස ශිෂ්යයා.
ක්රමය 1: TRUST.NORM ශ්රිතය
ක්රියාකරු TRUST.NORM, සංඛ්යානමය ශ්රිත සමූහයට අයත්, ප්රථම වරට එක්සෙල් 2010 දී දර්ශනය විය. මෙම වැඩසටහනේ පෙර සංස්කරණ වලදී, එහි ප්රතිසම භාවිතා වේ විශ්වාස කරන්න. මෙම ක්රියාකරුගේ කර්තව්යය වන්නේ සාමාන්ය ජනගහනය සඳහා සාමාන්ය බෙදාහැරීමක් සමඟ විශ්වාසනීය පරතරය ගණනය කිරීමයි.
එහි වාක්ය ඛණ්ඩය පහත පරිදි වේ:
= TRUST.NORM (ඇල්ෆා; සම්මත_අව; ප්රමාණය)
ඇල්ෆා - විශ්වාසනීය මට්ටම ගණනය කිරීම සඳහා භාවිතා කරන වැදගත්කම මට්ටම දැක්වෙන තර්කයක්. විශ්වාසනීය මට්ටම පහත දැක්වෙන ප්රකාශනයට සමාන වේ:
(1- "ඇල්ෆා") * 100
"සම්මත අපගමනය" - මෙය තර්කයක් වන අතර එහි සාරය නාමයෙන් පැහැදිලි වේ. යෝජිත නියැදියේ සම්මත අපගමනය මෙයයි.
"ප්රමාණය" - නියැදියේ ප්රමාණය තීරණය කරන තර්කයක්.
මෙම ක්රියාකරුට සියලු තර්ක අවශ්ය වේ.
ක්රියාකාරිත්වය විශ්වාස කරන්න පෙර තර්කයට සමාන තර්ක හා හැකියාවන් ඇත. එහි වාක්ය ඛණ්ඩය පහත පරිදි වේ:
= TRUST (ඇල්ෆා; සම්මත_අව; ප්රමාණය)
ඔබට පෙනෙන පරිදි, වෙනස්කම් ඇත්තේ ක්රියාකරුගේ නමින් පමණි. නිශ්චිත ශ්රිතය එක්සෙල් 2010 දී සහ අනුකූලතා අරමුණු සඳහා විශේෂ කාණ්ඩයක නවතම අනුවාද වල ඉතිරිව ඇත. "අනුකූලතාව". එක්සෙල් 2007 සහ ඊට පෙර සංස්කරණ වලදී, එය සංඛ්යානමය ක්රියාකරුවන්ගේ ප්රධාන කණ්ඩායමේ දක්නට ලැබේ.
විශ්වාසනීය පරතරයේ මායිම තීරණය වන්නේ පහත දැක්වෙන ආකෘතියේ සූත්රය භාවිතා කරමිනි:
X + (-) TRUST.NORM
කොහෙද X. යනු තෝරාගත් පරාසය මධ්යයේ පිහිටා ඇති සාමාන්ය නියැදි අගයයි.
දැන් අපි නිශ්චිත උදාහරණයක් භාවිතා කරමින් විශ්වාසනීය පරතරය ගණනය කරන්නේ කෙසේදැයි සොයා බලමු. පරීක්ෂණ 12 ක් සිදු කරන ලද අතර එහි ප්රති results ලයක් ලෙස විවිධ ප්රති results ල වගුවේ ලැයිස්තුගත කර ඇත. මෙය අපගේ සම්පූර්ණත්වයයි. සම්මත අපගමනය 8. විශ්වාසනීය පරතරය 97% ක විශ්වාසනීය මට්ටමකින් ගණනය කළ යුතුය.
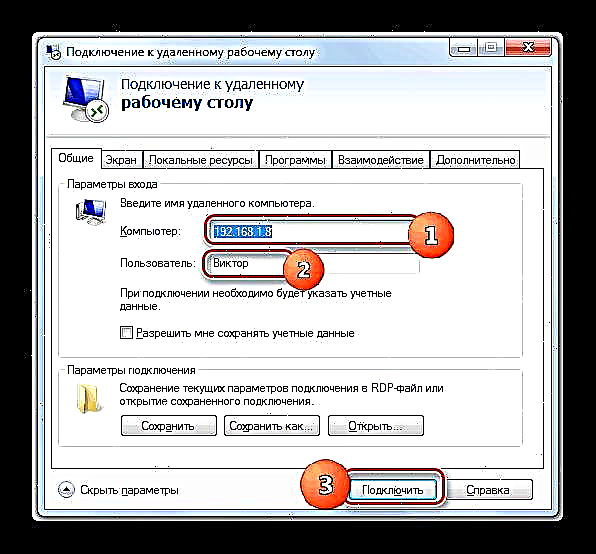
- දත්ත සැකසීමේ ප්රති result ලය පෙන්වන කොටුව තෝරන්න. බොත්තම මත ක්ලික් කරන්න "කාර්යය ඇතුළු කරන්න".
- පෙනී යයි විශේෂාංග විශාරද. ගණයට යන්න "සංඛ්යානමය" නම තෝරන්න TRUST.NORM. ඊට පසු, බොත්තම මත ක්ලික් කරන්න "හරි".
- තර්ක කොටුව විවෘත වේ. එහි ක්ෂේත්ර ස්වාභාවිකවම තර්කවල නම් වලට අනුරූප වේ.
කර්සරය පළමු ක්ෂේත්රයට සකසන්න - ඇල්ෆා. මෙහිදී අප වැදගත්කමේ මට්ටම දැක්විය යුතුය. අපට මතක ඇති පරිදි, අපගේ විශ්වාසනීය මට්ටම 97% කි. ඒ අතරම, එය ගණනය කරනු ලබන්නේ මේ ආකාරයට බව අපි කීවෙමු.(1- "ඇල්ෆා") * 100එබැවින්, වැදගත්කමේ මට්ටම ගණනය කිරීම සඳහා, එනම් වටිනාකම තීරණය කිරීම ඇල්ෆා ඔබ මේ ආකාරයේ සූත්රයක් යෙදිය යුතුය:
(1 මට්ටමේ විශ්වාසය) / 100එනම්, අගය ආදේශ කිරීමෙන්, අපි ලබා ගන්නේ:
(1-97)/100සරල ගණනය කිරීම් වලින් අපි සොයා ගන්නේ තර්කයයි ඇල්ෆා සමාන වේ 0,03. ක්ෂේත්රයේ මෙම අගය ඇතුළත් කරන්න.
ඔබ දන්නා පරිදි, කොන්දේසිය අනුව සම්මත අපගමනය වේ 8. එබැවින් ක්ෂේත්රයේ "සම්මත අපගමනය" මෙම අංකය ලියා තබන්න.
ක්ෂේත්රයේ "ප්රමාණය" ඔබට පරීක්ෂණවල අංග ගණන ඇතුළත් කළ යුතුය. අපට ඒවා මතක ඇති පරිදි 12. නමුත් සූත්රය ස්වයංක්රීය කිරීම සහ නව පරීක්ෂණයක් සිදු කරන සෑම අවස්ථාවකම එය සංස්කරණය නොකිරීම සඳහා, මෙම අගය සාමාන්ය අංකයකින් නොව ක්රියාකරුගේ සහාය ඇතිව සකසමු ගිණුම. එබැවින්, කර්සරය ක්ෂේත්රයේ සකසන්න "ප්රමාණය", ඉන්පසු සූත්ර රේඛාවේ වම්පස පිහිටා ඇති ත්රිකෝණය මත ක්ලික් කරන්න.
මෑතකදී භාවිතා කළ විශේෂාංග ලැයිස්තුවක් දිස්වේ. ක්රියාකරු නම් ගිණුම ඔබ මෑතකදී භාවිතා කළ, එය මෙම ලැයිස්තුවේ තිබිය යුතුය. මෙම අවස්ථාවේදී, ඔබට අවශ්ය වන්නේ එහි නම මත ක්ලික් කිරීමයි. ප්රතිවිරුද්ධ අවස්ථාවෙහිදී, ඔබ එය සොයා නොගත්තොත්, යන්න "වෙනත් විශේෂාංග ...".
- දැනටමත් අපට හුරුපුරුදු බව පෙනේ විශේෂාංග විශාරද. නැවතත් අපි කණ්ඩායමට යමු "සංඛ්යානමය". අපි එහි නම තෝරා ගනිමු "ගිණුම". බොත්තම මත ක්ලික් කරන්න "හරි".
- ඉහත ප්රකාශයේ තර්ක කවුළුව දිස්වේ. මෙම ශ්රිතය සැලසුම් කර ඇත්තේ සංඛ්යාත්මක අගයන් අඩංගු නිශ්චිත පරාසයේ ඇති සෛල ගණන ගණනය කිරීම සඳහා ය. එහි වාක්ය ඛණ්ඩය පහත පරිදි වේ:
= COUNT (අගය 1; අගය 2; ...)තර්ක සමූහය "වටිනාකම්" යනු සංඛ්යාත්මක දත්තවලින් පුරවා ඇති සෛල ගණන ගණනය කිරීමට ඔබට අවශ්ය පරාසය වෙත සබැඳියකි. සමස්තයක් වශයෙන්, එවැනි තර්ක 255 ක් දක්වා තිබිය හැකි නමුත් අපගේ නඩුවේදී අවශ්ය වන්නේ එකක් පමණි.
ක්ෂේත්රය තුළ කර්සරය සකසන්න "අගය 1" වම් මූසික බොත්තම අල්ලාගෙන, අපගේ ජනගහනය අඩංගු පත්රයේ පරාසය තෝරන්න. එවිට ඔහුගේ ලිපිනය ක්ෂේත්රය තුළ දර්ශනය වේ. බොත්තම මත ක්ලික් කරන්න "හරි".
- ඊට පසු, යෙදුම ගණනය කිරීම සිදු කර ප්රති the ලය එය පිහිටා ඇති කොටුව තුළ පෙන්වනු ඇත. අපගේ විශේෂිත අවස්ථාවෙහිදී, සූත්රය පහත දැක්වෙන ආකාරයෙන් වේ:
= TRUST.NORM (0.03; 8; ගිණුම (B2: B13))මුළු ගණනය කිරීමේ ප්රති result ලය විය 5,011609.
- නමුත් එපමණක් නොවේ. අපට මතක ඇති පරිදි, විශ්වාසනීය පරතරයේ මායිම ගණනය කරනු ලබන්නේ ගණනය කිරීමේ ප්රති result ලයේ සාමාන්ය නියැදි අගයෙන් එකතු කිරීම හා අඩු කිරීමෙනි. TRUST.NORM. මේ ආකාරයට, විශ්වාසනීය පරතරයේ දකුණු හා වම් මායිම් ඒ අනුව ගණනය කෙරේ. ක්රියාකරු භාවිතා කර සාමාන්ය නියැදි අගය ගණනය කළ හැකිය. AVERAGE.
මෙම ක්රියාකරු සැලසුම් කර ඇත්තේ තෝරාගත් සංඛ්යා පරාසයක අංක ගණිතය ගණනය කිරීම සඳහා ය. එයට පහත සඳහන් තරමක් සරල වාක්ය ඛණ්ඩයක් ඇත:
= AVERAGE (අංක 1; අංක 2; ...)තර්කය "අංකය" එය වෙනම සංඛ්යාත්මක අගයක් හෝ සෛල වෙත සබැඳියක් හෝ ඒවා අඩංගු සම්පූර්ණ පරාසයන් විය හැකිය.
එබැවින්, සාමාන්ය අගය ගණනය කරන කොටුව තෝරන්න, බොත්තම ක්ලික් කරන්න "කාර්යය ඇතුළු කරන්න".
- විවෘත වේ විශේෂාංග විශාරද. නැවත ගණයට යාම "සංඛ්යානමය" ලැයිස්තුවෙන් නම තෝරන්න SRZNACH. සෑම විටම මෙන්, බොත්තම මත ක්ලික් කරන්න "හරි".
- තර්ක කවුළුව ආරම්භ වේ. ක්ෂේත්රය තුළ කර්සරය සකසන්න "අංක 1" වම් මූසික බොත්තම එබීමෙන්, සම්පූර්ණ අගයන් තෝරන්න. ක්ෂේත්රයේ ඛණ්ඩාංක දර්ශනය වූ පසු, බොත්තම ක්ලික් කරන්න "හරි".
- ඊට පස්සේ AVERAGE ගණනය කිරීමේ ප්රති result ලය පත්ර මූලද්රව්යයක පෙන්වයි.
- විශ්වාසනීය පරතරයේ නිවැරදි සීමාව අපි ගණනය කරමු. මෙය සිදු කිරීම සඳහා, වෙනම කොටුවක් තෝරන්න, ලකුණක් තබන්න "=" ශ්රිත ගණනය කිරීම්වල ප්රති results ල පිහිටා ඇති පත්රිකා මූලද්රව්යවල අන්තර්ගතය එකතු කරන්න AVERAGE සහ TRUST.NORM. ගණනය කිරීම සිදු කිරීම සඳහා, බොත්තම ක්ලික් කරන්න ඇතුලත් කරන්න. අපගේ නඩුවේදී, පහත දැක්වෙන සූත්රය ලබා ගන්නා ලදී:
= F2 + A16ගණනය කිරීමේ ප්රති result ලය: 6,953276
- එලෙසම, අපි විශ්වාසනීය පරතරයේ වම් සීමාව ගණනය කරන්නේ ගණනය කිරීමේ ප්රති result ලයෙන් මෙවර පමණි AVERAGE ක්රියාකරු ගණනය කිරීමේ ප්රති result ලය අඩු කරන්න TRUST.NORM. එය පහත දැක්වෙන වර්ගයට අපගේ උදාහරණය සඳහා සූත්රය සපයයි:
= F2-A16ගණනය කිරීමේ ප්රති result ලය: -3,06994
- විශ්වාසනීය පරතරය ගණනය කිරීම සඳහා වූ සියලු පියවර විස්තරාත්මකව විස්තර කිරීමට අපි උත්සාහ කළෙමු, එබැවින් අපි සෑම සූත්රයක්ම විස්තරාත්මකව විස්තර කළෙමු. නමුත් ඔබට සියලු ක්රියා එක් සූත්රයකින් ඒකාබද්ධ කළ හැකිය. විශ්වාසනීය පරතරයේ නිවැරදි මායිම ගණනය කිරීම පහත පරිදි ලිවිය හැකිය:
= AVERAGE (B2: B13) + TRUST.NORM (0.03; 8; ගිණුම (B2: B13)) - වම් මායිමෙහි සමාන ගණනය කිරීමක් මෙසේ පෙනේ:
= AVERAGE (B2: B13) - TRUST.NORM (0.03; 8; ගිණුම (B2: B13))














ක්රමය 2: විශ්වාස ශිෂ්ය කාර්යය
ඊට අමතරව, එක්සෙල් හි විශ්වාසනීය පරතරය ගණනය කිරීම හා සම්බන්ධ තවත් ශ්රිතයක් ඇත - විශ්වාස ශිෂ්යයා. එය දර්ශනය වූයේ එක්සෙල් 2010 සිට පමණි. මෙම ක්රියාකරු ශිෂ්ය බෙදාහැරීම භාවිතා කරමින් ජනගහනයේ විශ්වාසනීය පරතරය ගණනය කරයි. විචලනය සහ ඒ අනුව සම්මත අපගමනය නොදන්නා විට භාවිතා කිරීම ඉතා පහසුය. ක්රියාකරු සින්ටැක්ස් පහත පරිදි වේ:
= විශ්වාස ශිෂ්යයා (ඇල්ෆා; සම්මත_අවසානය; ප්රමාණය)
ඔබට පෙනෙන පරිදි, මෙම නඩුවේ ක්රියාකරුවන්ගේ නම් නොවෙනස්ව පැවතුනි.
පෙර ක්රමයේදී අප සලකා බැලූ සමස්ථයේම උදාහරණය භාවිතා කරමින් නොදන්නා සම්මත අපගමනය සමඟ විශ්වාසනීය පරතරයේ මායිම් ගණනය කරන්නේ කෙසේදැයි බලමු. අවසාන වරට මෙන් විශ්වාසයේ මට්ටම 97% කි.
- ගණනය කරනු ලබන කොටුව තෝරන්න. බොත්තම මත ක්ලික් කරන්න "කාර්යය ඇතුළු කරන්න".
- විවෘත කළ විට ක්රියාකාරී විශාරද ගණයට යන්න "සංඛ්යානමය". නමක් තෝරන්න DOVERIT.STUDENT. බොත්තම මත ක්ලික් කරන්න "හරි".
- නිශ්චිත ක්රියාකරුගේ තර්ක කවුළුව දියත් කෙරේ.
ක්ෂේත්රයේ ඇල්ෆා, විශ්වාසනීය මට්ටම 97% ක් බව සලකමින්, අපි අංකය ලියන්නෙමු 0,03. දෙවන වරට අපි මෙම පරාමිතිය ගණනය කිරීමේ මූලධර්ම මත වාසය නොකරමු.
ඊට පසු, කර්සරය ක්ෂේත්රය තුළ සකසන්න "සම්මත අපගමනය". මෙවර මෙම දර්ශකය අප නොදන්නා අතර ගණනය කළ යුතුය. මෙය විශේෂ ශ්රිතයක් භාවිතයෙන් සිදු කෙරේ - STANDOTLON.V. මෙම ක්රියාකරුගේ කවුළුව විවෘත කිරීමට, සූත්ර තීරුවේ වම්පස ඇති ත්රිකෝණය මත ක්ලික් කරන්න. ලැයිස්තුවට අපේක්ෂිත නම සොයාගත නොහැකි නම්, යන්න "වෙනත් විශේෂාංග ...".
- ආරම්භ වේ විශේෂාංග විශාරද. අපි ගණයට යමු "සංඛ්යානමය" එහි නම සලකුණු කරන්න STANDOTKLON.V. ඉන්පසු බොත්තම මත ක්ලික් කරන්න "හරි".
- තර්ක කවුළුව විවෘත වේ. ක්රියාකරුගේ කාර්යය STANDOTLON.V යනු නියැදියේ සම්මත අපගමනය තීරණය කිරීමයි. එහි වාක්ය ඛණ්ඩය මේ වගේ ය:
= ලිංගාශ්රිත රෝග බී (අංක 1; අංක 2; ...)තර්කය අනුමාන කිරීම පහසුය "අංකය" තේරීමේ අයිතමයේ ලිපිනය වේ. තේරීම තනි අරාවකට තබා තිබේ නම්, ඔබට එක් තර්කයක් පමණක් භාවිතා කරමින් මෙම පරාසයට සබැඳියක් ලබා දිය හැකිය.
ක්ෂේත්රය තුළ කර්සරය සකසන්න "අංක 1" සෑම විටම මෙන්, වම් මූසික බොත්තම අල්ලාගෙන ජනගහනය තෝරන්න. ඛණ්ඩාංක ක්ෂේත්රය තුළ ඇති පසු, බොත්තම එබීමට ඉක්මන් නොවන්න "හරි", ප්රති result ලය වැරදියි. පළමුව අපි ක්රියාකරු තර්ක කවුළුව වෙත ආපසු යා යුතුය විශ්වාස ශිෂ්යයාඅවසාන තර්කය ඉදිරිපත් කිරීමට. මෙය සිදු කිරීම සඳහා, සූත්ර තීරුවේ සුදුසු නම ක්ලික් කරන්න.
- දැනටමත් හුරුපුරුදු ශ්රිතයක තර්ක කවුළුව නැවත විවෘත වේ. ක්ෂේත්රය තුළ කර්සරය සකසන්න "ප්රමාණය". නැවතත්, ක්රියාකරුවන්ගේ තේරීම වෙත යාමට අපට දැනටමත් හුරුපුරුදු ත්රිකෝණය මත ක්ලික් කරන්න. ඔබ තේරුම් ගත් පරිදි, අපට නමක් අවශ්යයි "ගිණුම". පෙර ක්රමයේ ගණනය කිරීම් වලදී අපි මෙම ශ්රිතය භාවිතා කළ බැවින් එය මෙම ලැයිස්තුවේ ඇත, එබැවින් එය මත ක්ලික් කරන්න. ඔබ එය සොයා නොගත්තේ නම්, පළමු ක්රමයේ විස්තර කර ඇති ඇල්ගොරිතම අනුගමනය කරන්න.
- වරක් තර්ක කවුළුව තුළට ගිණුමකර්සරය ක්ෂේත්රයට දමන්න "අංක 1" මූසික බොත්තම තද කර තබාගෙන අපි කට්ටලය තෝරා ගනිමු. ඉන්පසු බොත්තම මත ක්ලික් කරන්න "හරි".
- ඊට පසු, වැඩසටහන විශ්වාසනීය පරතරයේ අගය ගණනය කර පෙන්වයි.
- සීමාවන් තීරණය කිරීම සඳහා, අපි නැවතත් නියැදියේ සාමාන්ය අගය ගණනය කළ යුතුය. නමුත්, සූත්රය භාවිතා කරමින් ගණනය කිරීමේ ඇල්ගොරිතම ලබා දී ඇත AVERAGE පෙර ක්රමයට සමාන වන අතර ප්රති result ලය පවා වෙනස් වී නැතත් අපි දෙවන වරටත් මේ පිළිබඳව වාසය නොකරමු.
- ගණනය කිරීමේ ප්රති .ල එකතු කිරීම AVERAGE සහ විශ්වාස ශිෂ්යයා, අපි විශ්වාසනීය පරතරයේ නිවැරදි සීමාව ලබා ගනිමු.
- ක්රියාකරුගේ ගණනය කිරීමේ ප්රති results ල වලින් අඩු කිරීම AVERAGE ගණනය කිරීමේ ප්රති .ලය විශ්වාස ශිෂ්යයා, අපට විශ්වාසනීය පරතරයේ වම් සීමාව ඇත.
- ගණනය කිරීම එක් සූත්රයකින් ලියා ඇත්නම්, අපගේ නඩුවේ දකුණු මායිම ගණනය කිරීම මේ ආකාරයෙන් පෙනෙනු ඇත:
= AVERAGE (B2: B13) + TRUST. STUDENT (0.03; STD CLIP. B (B2: B13); ACCOUNT (B2: B13)) - ඒ අනුව, වම් මායිම ගණනය කිරීමේ සූත්රය මේ ආකාරයෙන් පෙනෙනු ඇත:
= AVERAGE (B2: B13) - විශ්වාස ශිෂ්යයා (0.03; STD CLIP. B (B2: B13); ගිණුම (B2: B13))













ඔබට පෙනෙන පරිදි, විශ්වාසනීය පරතරය සහ එහි සීමාවන් ගණනය කිරීමට එක්සෙල් මෙවලම් සැලකිය යුතු ලෙස පහසුකම් සපයයි. මෙම අරමුණු සඳහා, විචලනය දන්නා සහ නොදන්නා සාම්පල සඳහා වෙනම ක්රියාකරුවන් භාවිතා කරයි.